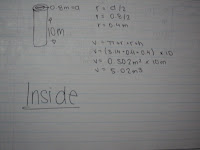Marie's Algebra Post

One-step Equations

In order for you to understand the steps, there are a couple of words you need to know.
a

Variable - the unknown

-use a letter to represent a number

Constant - the integer in an algebraic expression or equation

Addition/Subtraction

1. Isolate the variable
2. Cancel using the opposite operation *create a zero pair for the constant*
3. Balance on the other side of the equal sign
4. Verify your answer

Example:

Multiplication/Division

1. Isolate the variable
2. Cancel using the opposite operation
3. Balance
4. Verify

Example:

Alge-tiles

Addition/Subtraction

Multiplication/Division

Here is a link for one-step equations.

This video helps solve one-step equations.

Two-Step Equations

Steps:

1. Isolate the variable
2. Cancel the constant
3. Balance
4. Simplify variable
5. Balance
6. Verify

Example:

Here is a link for two-step equations.

This video shows how to solve two-step equations.

*Sorry for the boring, black font. My browser won't let me use colours, and it messed up.

Term 2 Reflection

Hi, my name is Marie Domingo and I’m here to talk about my term 2 reflection. I did well on the percent unit because it was the easiest for me. The percent problems took me at least 2 minutes to finish each. I understood it so fast! Also, I perfected most of my tests and quizzes. One thing I struggled with at first were making nets for prisms and cylinders. Even if Mr. Harbeck taught us how to draw them, it still confused me. But by lots of practice, I was able to draw nets more quickly and accurately. Next term, I will try to ask more questions and further my answers. Also, I want to perfect all my tests and quizzes.

In term 2, we learned about getting the percent of numbers and how to solve percent word problems. One method I really liked was using t-charts. Also, we converted fractions, decimals, and percents. I didn’t understand how to convert them at first, but after a while I was able to get it.

Another unit we focused on was surface area. All 3D objects are measured in square units. We learned how to make nets of prisms and cylinders using grid paper. A net turns a 3D object into a 2D object. A rectangular prism has 6 faces, and each face is a rectangle. There is a front, side, and top view of each rectangular prism. A triangular prism has 5 faces. 3 of the faces are rectangles while 2 of them are triangles. A cylinder has 3 faces. 2 are circles, and one of them is a rectangle. As I said, the hardest for me was making the nets. It was difficult to transform a 3D object into a 2D object containing all sides. Though, I was able to understand it after doing a few more nets!

The last thing we learned in term 2 was volume. The volume of an object is how much space the object can take. The formula to find the volume is v = area of base x height. For a rectangular prism, you would have to multiply the length and width together to find the area of base. For a triangular prism, the formula would be base x height / 2 x height. The base of the triangular prism is a triangle, and it cannot be anything else. For a cylinder, the formula to find the volume would be v = pi r r h x height. I didn’t have any trouble with this unit. This one was pretty easy to understand.

The difference between surface area and volume is that surface area is the area of the prism or cylinder’s faces. Volume is the area of how much an object can take. Basically, surface area is the area of the outside, and volume is the area of the inside.

Marie's Great Big Book of Integers

Chapter 1 Grade 7 Integer Review

(+4) + (-2) = 2

+4 = positive 4, have 4

+ = and
-2 = negative 2, owe 2

Have 4 and Owe 2 = Have 2

Standard Form

4 - 2 = 2

Make zero pairs:

-16 +16

-5 +5

-11 +11

-2 +2

+6 -6

-10 +10

-9 +9

-5 +5

-6 +2 = -4

-6 -2 = -8

-6 +10 = +4

6 - (-4) = 10

-2 - (-3) = 1

-3 -6 = -9

-3 -2 = -5

3 -2 = Subtraction = adding a negative integer

Homework:

-6 - (-4) = -2

-10 +6 = -4

6 -7 +2 = +1

14 - (-3) = +17

-3 - (-7) = +4

-3 -7 = -10

3 -7 = -4

3 +7 = +10

Chapter 2: Multiplying Integers

(+2)x(+3) = +6

(2)x(3) = 6

(2)(3) = 6 *Standard form*

2(3) = 6

(+2)x(+3) = +6

or 2 groups of (+3)

(+2)x(-3) = -6

or 2 groups of (-3)

(-2)x(-3) = +6

or remove 2 groups of (-3)

(-2)x(+3) = -6

or remove 2 groups of (+3)

Sign Rule (negative signs):

Even = When you have an even number of negative factors, the product is positive.

Odd = When you have an odd number of negative factors, the product is negative.

Chapter 3: Dividing Integers

Partitive Division or making parts:

6 ÷ 2 = How many groups of (+2) are in 6?

There are 3 groups of 2 in 6.

(-6) ÷ (-2) = How many groups of (-2) are in -6?

There are 3 groups of (-2) in -6.

Quotative Division or sharing your total with groups.

(-6) ÷ 2 = Share -6 with 2 groups.

6÷2= and -6÷ (-2)= will be positive because if you have no negative or an even number of negative signs in a division question, the quotient is positive.

(-6)÷2= and 6÷(-2)= will be negative because when you have an odd number of negative signs in a division question, the quotient is negative.

Chapter 4: Order of Operations with Integers

BEDMAS = Brackets, Exponents, Division, Multiplication, Addition, Subtraction

(+5) x (-3) + (-6) ÷ (+3)=

First, you would need to use square brackets to separate the equation.

[ (+5) x (-3) ] + [ (-6) ÷ (+3) ] =

This step causes the equation easier to solve.

Next, you solve what's inside the square brackets.

(-15) + (-2) =

The answer should be -17.

Marie's Volume Post

Things to remember:

• The bases are circles
• Radius is half a diameter
• Diameter cuts a circle in half
• Circumference is the perimeter of a circle
• Pi is the ratio between circumference/diameter or 3.14

Formulas:
Circumference - pi (d) = c
Radius - d/2 = r
Diameter - 2r = d or c/pi

Area of a circle:
pi (r²) or pi (r) (r)

Net of a cylinder:

Formula:
lxw = a
pi (r) (r) = a
d = 2r
r = d/2
c = pi(d)

Here are the answers on our homework.
*I'm only showing one of each (diameter, circumference, radius) because Mr. Harbeck told me to.*

Here is a link on cylinders.

A video to help you learn the surface area of a cylinder:

Cylinder Volume and Volume Problems


7.3

7.4

Marie's Final Percent Post

Percent means out of 100, and can be expressed as decimals or fractions. Also, it is another name for hundredths.

4.1 Representing Percents:

One fully shaded in grid equals to 100%. If you want to show a percent larger than 100%, shade in more than one grid. To represent a percent less than 1%, colour in part of one square. Shade in squares to represent the whole number, and shade in part of a square to show the fraction.

4.2 Fractions, Decimals, & Percents:

Percents can be written as decimals and fractions.

For example,

25% = 0.25 = 25/100 or 1/4

4.3 Percent of a number:

To find the percents of some numbers, you can use mental math strategies such as halving, doubling, or dividing by ten.

Write the percent as a decimal then multiply by the number to calculate the percent.

For example,

350% of 10 = 3.50 x 10 = 35

4.4 Combining Percents:

Percents can be combined by adding to solve percents.

Eg. 5% + 7% = 12%

To calculate the increase in a number you can:

Add combined percent to the original number.

12% of 100 = 0.12 × 100 = 12

100 + 12 = 11

Multiply the original number by a single percent greater than 100.

112% of 100 = 1.12 × 100 = 112

Percents of percents can be used to determine amounts that result from consecutive percent increases or decreases.

My Percent Review Video

For this unit, I did one percent scribe post.

Here is a link on percentages.

Marie's Pay It Forward

Part 1:
Pay it forward is an idea that a young boy named Trevor thought of. It was a school project, where you help 3 people, but expect nothing in return. Instead, they help 3 other people, and so on. It's like a tree. If each person helped 3 other people, the number will increase.

Part 2:
My group (Diorella, Julibella, Angel, and Marilen) and I paid it forward by buying toys and donating them to the Children's hospital. Also, we're giving out candy canes, attached with a card that says, "You've been hit by a random act of kindness. Pay it forward!" to people at Polo Park. I chose this activity because we know how sad it is to stay at the hospital and not going out. The toys will give them happiness and joy. The whole event happened on December 18, 2010.





Part 3:

During our Pay it Forward event, we went to the Children's Hospital to drop off the toys. We gave the bag of toys to the nurse and took a picture with her. I felt great because I did something to help the children who don't normally go out. At least the toys will them joy and entertainment. The nurse was very thankful because they now have a new set of toys. We did not ask her to pay it forward because we left a card in the toy bag that said, "Pay it forward!".

At Polo Park, Diorella and I were dressed up as an elf and Santa Claus. As we were ready to hand out the candy canes, the security told us we needed permission, otherwise we were not allowed. Though we were upset that our plan did not go out as what we expected, we figured out another way to "pay it forward"! At the parking lot of Polo Park, we placed the cards on people's windshields. Our group was really cold outside, but our hearts were warmth by the difference we made to help others.

Part 4:

The idea of Pay it Forward is important because it helps a lot of people, with the start of one person. Also, it isn't a hard concept to do because you're only helping 3 people, and the ones you helped do the same to 3 others. It makes people realize that one little thing can grow into one of the largest ideas in the world.

I do hope that my act of kindness made a difference because that will really feel amazing knowing I've helped someone.

Page 128: Representing Percents

For this scribe, I was assigned to do questions 3, 7, 11 and 13.


3. Shindi commented to a friend that “some percents would be easier to show if we shaded the parts that were not included in the percent.” Explain what she means. Which percents are easier to show using Shindi’s method? Why?

Shindi meant that for some percentages, it would be better to colour in the parts in a 10x10 grid that are not included in the percent because it will be easier to identify the percent.

7. Represent the percent in each statement on a grid.

a) Attendance at the fall fair increased by 3.2% this year.

b) The average mass of a Singapura cat is about 0.13% of the mass of a Siberian tiger.










c) The length of the Yukon River is about 230% of the length of the Fraser River.









11. The land area of Alberta is about 113% of the land area of Saskatchewan. Use hundred grids to show how the land area of Alberta compares with the land area of Saskatchewan.

Saskatchewan = 100%
Alberta = 113%















13.
a) Use a calculator to convert 1/3 to a decimal. How could 1/3% be shown using a hundred grid?

1/3 converted into a decimal is 0.3 repeated.







b) Why are percents involving repeating decimals sometimes difficult to show on a hundred grid?

Percents involving repeating decimals can be difficult because you need to know how to convert a repeated decimal onto a grid. Also, repeating decimals never end.


Here is a link on percents.

The video below helps you to find percentages.

Scribe 3

Page 84: Show You Know

Determine the side length of a square with an area of 196 cm².

I used prime factorization to answer this:




The side length of a square with an area of 196 cm squared is 14 cm².






Page 85: Questions 3, 7, 12 and 14.

3. The square root of 36 is 6 because out of all the factors, 6 multiplied by itself is the only one that equalled to 36.

7. a) 2x3x7 = 42 ; It is not a perfect square.
b) 13x13 = 169 ; It is a perfect square.
c) 2x2x2x2x2x2x2x2 = 256 ; It is a perfect square.

12. Determine the square of each number:
a) 3x3 = 9
b) 18x18 = 324

14. Determine the side length of a square with an area of 900cm²
900 ÷ 30 = 30 ; 30x30 = 900cm²
The side length of a square with an area of 900cm² is 30 cm.

Here is a video on square roots.


Here is a link on square roots.

Marie's Sesame Street Video

Group Members:
Diorella and I


Part 1:
Two term ratio: Compares 2 quantities measured in the same units. (eg. a:b)
Three term ratio: Compares 3 quantities measured in the same units. (eg. a:b:c)
Part to part ratio: Compares different parts of a group to each other. (eg. 1:3, c:d)
Part to whole ratio: Compares one part of the group to the whole group. It can be written as a fraction, decimal and percent. (eg. a:all letters, 5:10)

Rate: Compares 2 quantities measured in different units. (eg. 5m/3s)
Unit rate: A rate where the second term is 1. (eg. 3km/1hr)
Unit price: A rate used when shopping. (eg. $2/100g)

Proportional Reasoning: A relationship that says that 2 rates or ratios are equal. It can be written in fraction form. (eg. 1/2 = 2/4)


Part 2:
The original video was from Youtube. It is called "Sesame Street: Pretend Teeth"



This video is about Elmo and Abby pretending to brush their teeth.


Part 3:
Our remake of "Sesame Street: Pretend Teeth"



Our video is about ratios and the different kinds of examples.

Marie's Math Profile

Hello, my name is Marie and I take math in grade 8. When people ask me if I like math, I always say yes because it involves a lot of thinking. Math is one of my favourite subjects in school ever since grade 1. The best thing I have ever done in math class was probably fractions. It was the easiest to do when I was in grade 4, but it got harder and harder as I got older. I love adding and subtracting fractions. I remember one time I was in a group and we were given a big brownie the size of a math textbook. We had to divide it into 6 and we used it to make fractions. At the end, we got to eat it!

Last year in grade 7, I did my best working on algebraic equations. The order of operations was easy for me to understand, though it might have been hard for some people. I struggled the most in circle graphs. Converting the numbers to percents and degrees made it difficult for me to do. Sometimes, the word problems didn't make sense in my head. But, as I practiced it got easier. This year I will try to ask more questions from my peers and teacher so I wouldn't struggle as much.

I am in grade 8 now. To be a successful math student, I will do my homework as early as possible and not procrastinate. I remember doing that last year and it was a big mistake. I will also write in my agenda more often so I wouldn't forget to do my homework. This year I want to learn more about algebraic equations, and difficult word problems.

Last year I did a few blog posts. My favourite post I made was Range & Outliers. It was the last that I made and it showed how much I improved in blogging. Blogging helped me become a better student because I needed to listen and write notes in class to make sure I have everything to make a post. It helped me be more responsible. In computer class during math, I would love to go on math sites that I've never been to before. I heard that we would be making math videos, and I'm really looking forward to doing that!